If Variables Change In The Same Direction, What Type Of Correlation Is This Called?

Correlation in Data Scientific discipline

Office 1: Basic concepts of Correlation, Covariance and how to deal with Multicollinearity

Correlation has been ane of the important statistical tool while making a machine learning project. It is very of import to sympathise how independent variables are related to each other, how an contained variable and a dependent variable are related.

Information technology gives you an insight of data, it clarifes which feature tin be a obstruction in optimization of problem nosotros are working on.

Which feature to remove? Which feature is giving me the best model?

This article volition simplify the thought procedure behind Correlation and Why it ease the life of a Automobile Learning Engineer.

Topics nosotros will comprehend in this article:

1. What is Correlation and Co-Variance?
2. Why cull Correlation over Co-Variance?
3. What are the Ways to detect Correlation between Variable?
4. What are the types of Correlation?
5. What is the Problem of Multicollinearity?
6. What are the Remedies of Multicollinearity?

one.a CORRELATION

Correlation refers to the extent to which 2 variables have a linear relationship with each other. It is a statistical technique that tin show whether and how strongly variables are related. It is a scaled version of co-variance and values ranges from -one to +ane.

Variables within a data gear up can be related for lots of reasons.

• One variable could cause or depend on the values of another variable.
• Ane variable could be lightly associated with another variable.
• Two variables could depend on a third unknown variable.

It can be useful in data assay and modeling to amend sympathize the relationships between variables. The statistical relationship between 2 variables is referred to as their correlation. A correlation could exist positive, meaning both variables move in the same direction, or negative, meaning that when one variable's value increases, the other variables' values decrease. Correlation tin also be neural or zero, pregnant that the variables are unrelated.

• Positive Correlation: both variables change in the same management.
• Neutral Correlation: No relationship in the change of the variables.
• Negative Correlation: variables change in reverse directions.

one.b CO-VARIANCE

Variables can be related by a linear relationship. This is a relationship that is consistently additive across the two data samples.

This relationship tin can be summarized betwixt two variables, chosen the co-variance. It is calculated as the boilerplate of the product between the values from each sample, where the values haven been centered (had their mean subtracted).

The adding of the sample co-variance is as follows:

cov(X, Y) = (sum (10 — hateful(X)) * (y — mean(Y)) ) * one/(n-1)

The utilise of the hateful in the calculation suggests the need for each data sample to have a Gaussian or Gaussian-similar distribution.

The sign of the co-variance tin can be interpreted equally whether the two variables change in the same direction (positive) or change in different directions (negative). The magnitude of the co-variance is not easily interpreted. A co-variance value of zilch indicates that both variables are completely independent.

The cov() NumPy part can be used to calculate a co-variance matrix between two or more than variables.

co-variance = cov(data ane, data 2)

The diagonal of the matrix contains the co-variance between each variable and itself. The other values in the matrix represent the co-variance between the two variables; in this case, the remaining two values are the same given that we are calculating the co-variance for only two variables.

ii.WHY CHOOSE CORRELATION OVER CO-VARIANCE?

When it comes to making a pick, which is a better measure of the relationship betwixt two variables, correlation is preferred over covariance, considering it remains unaffected by the alter in location and calibration, and tin as well be used to make a comparing betwixt two pairs of variables.

three. What are the Ways to detect Correlation betwixt Variable?

Just an example how correlation matrix looks like

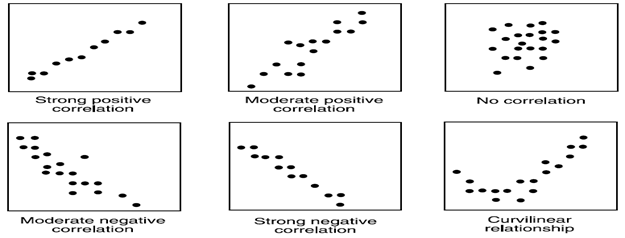
1. Graphical Method : While doing bi-variate analysis between two continuous variables, nosotros should expect at scatter plot. It is a bully way to find out the human relationship between two variables. The design of scatter plot indicates the relationship between variables. The relationship can be linear or non-linear.

Scatter plot shows the relationship between two variable merely does not indicates the strength of human relationship among them. To notice the strength of the relationship, nosotros utilise statistical technique.

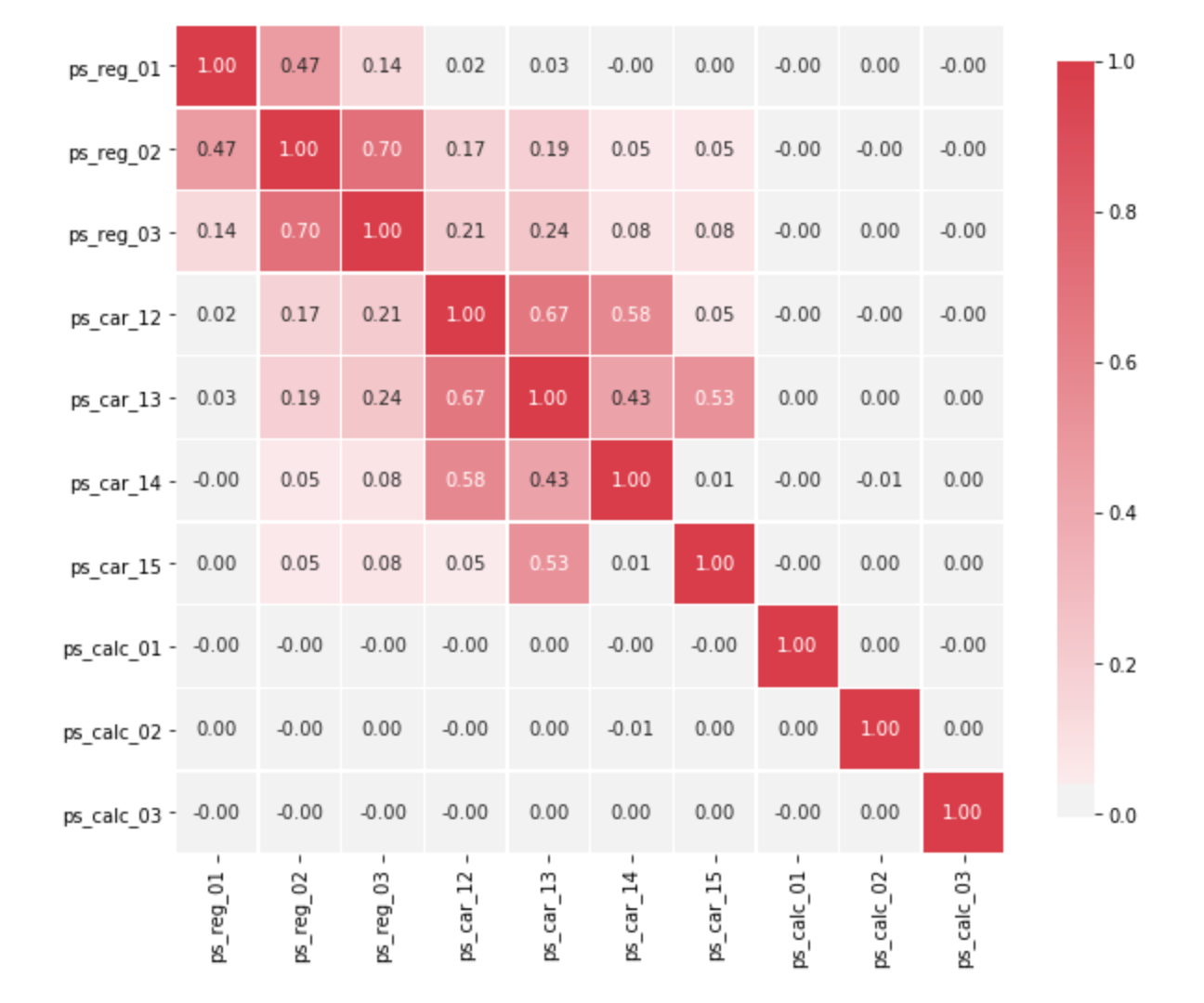
two. Non-graphical method: Build the correlation matrix to understand the forcefulness between variables. Correlation varies between -1 and +1.

a. -1: Perfect negative linear correlation

b. +i: Perfect positive linear correlation

c. 0: No correlation

Ideal assumptions:

ane. High Correlation between dependent and independent variable.

two. Less correlation betwixt independent variables.

Generally, if the correlation betwixt the two independent variables are high (>= 0.viii) then nosotros drop one independent variable otherwise information technology may lead to multi collinearity trouble. Various tools accept function or functionality to place correlation between variables. In Excel, part CORREL() is used to return the correlation between two variables and SAS uses procedure PROC CORR to place the correlation. These function returns Pearson Correlation value to identify the relationship betwixt two variables.

4.WHAT ARE TYPES OF CORRELATION?

1. PEARSON'South CORRELATION

The Pearson correlation coefficient (named for Karl Pearson) tin be used to summarize the strength of the linear relationship between 2 data samples.

The Pearson'south correlation coefficient is calculated as the co-variance of the 2 variables divided by the product of the standard departure of each data sample. It is the normalization of the co-variance between the 2 variables to give an interpretable score.

Pearson's correlation coefficient = co-variance(X, Y) / (stdv(X) * stdv(Y))

The utilise of hateful and standard departure in the calculation suggests the need for the two information samples to have a Gaussian or Gaussian-like distribution.

The result of the calculation, the correlation coefficient can be interpreted to empathize the human relationship.

The coefficient returns a value betwixt -1 and 1 that represents the limits of correlation from a full negative correlation to a full positive correlation. A value of 0 means no correlation. The value must be interpreted, where ofttimes a value below -0.5 or higher up 0.v indicates a notable correlation, and values below those values suggests a less notable correlation.

The pearsonr() SciPy part can exist used to summate the Pearson'due south correlation coefficient between two information samples with the same length.

The Pearson'south correlation coefficient can exist used to evaluate the human relationship between more than two variables.

This tin can exist done by calculating a matrix of the relationships between each pair of variables in the dataset. The consequence is a symmetric matrix called a correlation matrix with a value of 1.0 along the diagonal as each column e'er perfectly correlates with itself.

2. SPEARMAN'S CORRELATION

Ii variables may be related by a nonlinear human relationship, such that the relationship is stronger or weaker across the distribution of the variables.

Further, the 2 variables being considered may have a non-Gaussian distribution.

In this example, the Spearman's correlation coefficient (named for Charles Spearman) can be used to summarize the force between the two data samples. This test of relationship can as well be used if at that place is a linear relationship between the variables, but will have slightly less ability (e.g. may result in lower coefficient scores).

As with the Pearson correlation coefficient, the scores are between -1 and 1 for perfectly negatively correlated variables and perfectly positively correlated respectively.

Instead of calculating the coefficient using co-variance and standard deviations on the samples themselves, these statistics are calculated from the relative rank of values on each sample. This is a common arroyo used in not-parametric statistics, e.yard. statistical methods where we practise not presume a distribution of the information such equally Gaussian.

Spearman's correlation coefficient = co-variance(rank(X), rank(Y)) / (stdv(rank(X)) * stdv(rank(Y)))

A linear relationship betwixt the variables is not assumed, although a monotonic relationship is assumed. This is a mathematical name for an increasing or decreasing human relationship between the two variables.

If you lot are unsure of the distribution and possible relationships between 2 variables, Spearman correlation coefficient is a good tool to use.

The spearmanr() SciPy office can be used to calculate the Spearman's correlation coefficient betwixt 2 data samples with the same length.

Every bit with the Pearson's correlation coefficient, the coefficient can be calculated pair-wise for each variable in a dataset to give a correlation matrix for review.

5.What is the Problem of Multicollinearity?

Multicollinearity (also collinearity) is a phenomenon in which two or more predictor variables (Contained variables) in a regression model are highly correlated, meaning that one tin exist linearly predicted from the others with a substantial degree of accurateness. In this situation the coefficient estimates of the multiple regression may change erratically in response to small changes in the model or the data. Collinearity is a linear association between two explanatory variables. Two variables are perfectly collinear if there is an exact linear relationship betwixt them.

Types of multicollinearity:

There are two types of multicollinearity:

1. Structural multicollinearity is a mathematical artifact caused by creating new predictors from other predictors — such as, creating the predictor xtwo from the predictor x.

2. Information-based multicollinearity, on the other hand, is a result of a poorly designed experiment, reliance on purely observational data, or the inability to manipulate the system on which the data are collected.

Discover Multicollinearity:

Indicators that multicollinearity may be nowadays in a model include the following:

1. Big changes in the estimated regression coefficients when a predictor variable is added or deleted

ii. Insignificant regression coefficients for the affected variables in the multiple regression, just a rejection of the joint hypothesis that those coefficients are all nil (using an F-test)

3. If a multivariable regression finds an insignificant coefficient of a item explanator, even so a elementary linear regression of the explained variable on this explanatory variable shows its coefficient to be significantly different from zero, this situation indicates multicollinearity in the multivariable regression.

4. VIF (Variance aggrandizement cistron) tin exist used to detect multicollinearity in the regression model{\displaystyle \mathrm {tolerance} =1-R_{j}^{2},\quad \mathrm {VIF} ={\frac {ane}{\mathrm {tolerance} }},}

Why is this problem?

• Collinearity tends to inflate the variance of at least one estimated regression coefficient.

• This tin cause at to the lowest degree some regression coefficients to have the incorrect sign.

Means of dealing with collinearity

· Ignore it. If prediction of y values is the object of your study, then collinearity is non a problem.

· Become rid of the redundant variables past using variable sélection technique.

There are multiple techniques to select variables which are less correlated with high importance

ane. Correlation method

2. PCA (Chief Component Analysis)

3. SVD (Singular value Decomposition)

iv. Machine learning algorithms (Random Forest, Decision trees)

Remedies for multicollinearity

1. Drop one of the variables. An explanatory variable may be dropped to produce a model with significant coefficients. However, yous lose information (because you've dropped a variable). Omission of a relevant variable results in biased coefficient estimates for the remaining explanatory variables that are correlated with the dropped variable.

two. Obtain more information, if possible. This is the preferred solution. More information can produce more precise parameter estimates (with lower standard errors), equally seen from the formula in variance aggrandizement factor for the variance of the estimate of a regression coefficient in terms of the sample size and the degree of multicollinearity.

3. Try seeing what happens if you use independent subsets of your information for estimation and utilise those estimates to the whole data set up. Theoretically you should obtain somewhat college variance from the smaller data sets used for estimation, but the expectation of the coefficient values should be the same. Naturally, the observed coefficient values will vary, merely look at how much they vary.

iv. Standardize your independent variables. This may assistance reduce a simulated flagging of a condition index to a higher place 30.

5. Information technology has too been suggested that using the Shapley value a game theory tool, the model could account for the effects of multicollinearity. The Shapley value assigns a value for each predictor and assesses all possible combinations of importance.

6. If the correlated explanators are different lagged values of the same underlying explanator, then a distributed leg technique can exist used, imposing a general structure on the relative values of the coefficients to be estimated.

IN NEXT Office We Will Encounter HOW Tin can WE CODE CORREALTION IN PYTHON AND Will SEE CORREALTION MATRIX.

Nosotros WILL TALK Virtually Practical APPLICATIONS OF CORRELATION IN Real Globe PROBLEMS.

Source: https://medium.com/analytics-vidhya/why-correlation-ease-my-life-part-1-9aab20197d13

Posted by: ammonsmucithe.blogspot.com

Share this post